Image Transformation using Limited Reference with Application to Photo-Sketch Synthesis
Wei Bai,
Yanghao Li,
Jiaying Liu,
Zongming Guo
(click to contact us)
Published on VCIP, December 2014.
Introduction
Image transformation has been extensively studied in the last decade. Researchers find that many problems in computer vision can be addressed as transforming images from one style to another [1], i.e., cross-style transformation. The input and output image are visually different, but have the same content and are in registration with each other. It is worth pointing out that in this context "style" means a form of image instead of a specific image type. Typical applications such as image super-resolution, photo-sketch synthesis, and artistic rendering all belong to this category. Due to the fact that cross-style image transformation is widely demanded, solving this problem is of great practical importance. For example, photo-sketch synthesis is very popular in the forensic area for suspect identification. Besides, it can also help people understand how we observe the same scene with distinctive information physiologically.
It is often the case that people see a target style image and they want to transform their own image into the same style with the target image. Thus in most situations, the reference is limited. In this paper, we develop a general sparse representation based method for image transformation with limited reference and apply it to photo-sketch synthesis.
Image Transformation with Limited Reference
Conventional sparse representation based image transformation methods generate a target image $y$ from a corresponding input source $x$. They are usually composed of two stages, the learning stage and the reconstruction stage. In the learning stage, external image pairs (e.g., low-res and high-res image pairs and photo-sketch pairs) $\{X, Y\}$ are trained based on sparse representation. That is, \begin{equation} \label{eq:sparse repre.} \begin{split} &D_x = \arg\min_{D_x}\{X - D_{x}\Gamma\}_2^2 + \lambda||\Gamma||_1,\\ &D_y = \arg\min_{D_y}\{Y - D_{y}\Gamma\}_2^2 + \lambda||\Gamma||_1, \end{split} \end{equation} where $D_x$ and $D_y$ are coupled dictionaries, and $\Gamma$ denotes the sparse coefficients. Specifically, the underlying relations between training image pairs are learned in the sparse domain during training process. Therefore, in the reconstruction stage, an input source image $x$ is first sparse coded in the source style dictionary $D_x$ with coefficient $\gamma$, which relates the source style and the target style because they share the same coefficients in the sparse domain. So the output target image corresponding to the input source can be predicted by enforcing the sparse code $\gamma$ to the target style dictionary $D_y$, $y=D_y{\gamma}$.
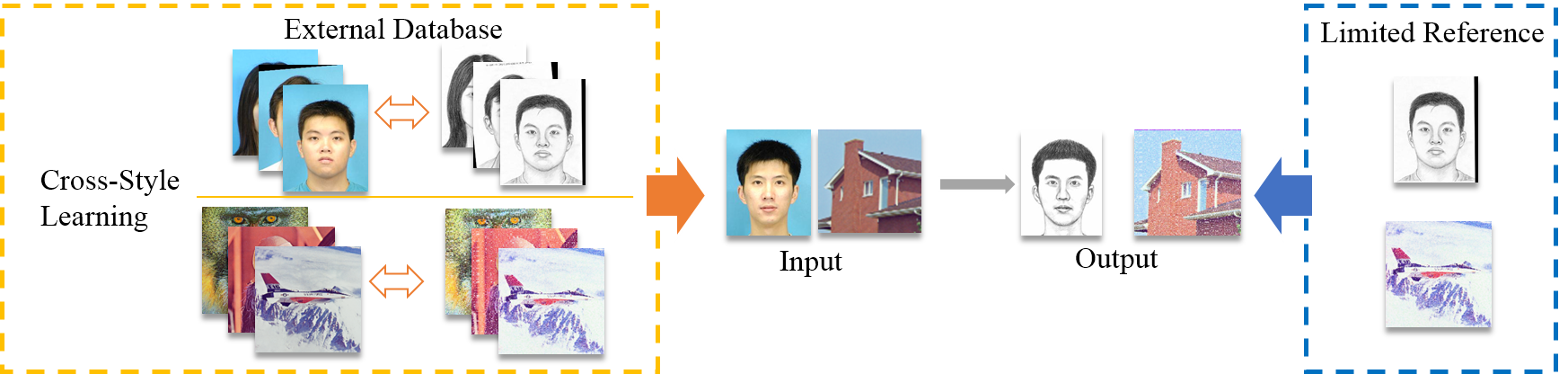
Fig.1 Simulated scenario vs. real-world scenario. Here we take photo-sketch synthesis and image super-resolution as examples.
As illustrated in Fig.1, the top-left part of the figure describes how external database facilitates the reconstruction process in conventional transformation methods. However, the fact is, in real-world applications, it is often the case that we only have limited reference, i.e., the top-right part in Fig.1. This means if there is a target style image $z$, we want to transform the input source image $x$ into the same style with $z$. Frequently, there are no external database like $\{X, Y\}$ to train dictionaries. Plus, $z$ is not necessarily $x$'s counterpart. We know it is critical to build mapping relations between different style images. But in this circumstance, there are no image pairs to train such mapping relations. Thus the problem is how to learn the relation between different styles under the limited-reference situation. We will elaborate on this problem in the following section.
How to Match Image Patches of Different Style?
It is very difficult to learn mappings between inconsistent single images unless we can build corresponding training pairs with them. Hence, our solution to the limited-reference problem is creating a paired image patch database from the limited reference. It leaves us to find similar patches between $x$ and $z$, i.e., the source input image and the target style image. These similar patches, or nearest neighbors (NNs) should meet the following requirement, distributed in different styles but similar in content. Therefore we need to develop a feature that can relate the true similar image patches of different style.
Intuitively, we come up with the edge feature to relate two style images. It origins from the observation that edges rarely decay between styles since they are the most important features for visual cognitive tasks. Another reason is relative to the a recent work [2], which suggests that it is possible to build a dictionary for edge patches as opposed to intensity patches.
These facts motivate us to build a dictionary for coupled edge patches with the limited reference. To build edge patch based dictionary, edge preserving filters are applied on reference images. The smoothed image is subsequently subtracted from the original image to obtain an edge image which captures the edges well. Therefore edge features can be used to map patches between different style images for coupled dictionary learning. In this work we suggest using the guided image filter [3]. Let $g$ be the image to be filtered and $h$ be the filtered output. Using the input image as guidance image $I$, the filtering output at a pixel $i$ can be expressed as a weighted average: \begin{equation} \label{eq:wtsum} h_i=\Sigma_{j}W_{i,j}(I)g_j, \end{equation} where $i$ and $j$ represent pixel indexes. The filter kernel $W_{i,j}$ is a function of the guidance image, taking the form as: \begin{equation} \label{eq:guidedfilter} W_{i,j}=\frac{1}{|\omega|^2}\sum_{k:(i,j)\in{\omega_{k}}}(1+\frac{(I_i-\mu_{k})(I_j-\mu_{k})}{\sigma_k^2+\epsilon}) \end{equation} where $\mu_{k}$ and $\sigma_{k}$ denote the mean and the variance of $I$ in a $r\times{r}$ window $\omega_{k}$. Pixel $k$ is the center of window $\omega_{k}$ and $|\omega|$ stands for the number of pixels in this window. $\epsilon$ is a smoothness parameter. To demonstrate how the filter kernel preserve edges of $I$ in the output, we take a 1-D step edge for example. If $I_j$ and $I_i$ are on the same side of an edge, $(I_i-\mu_{k})(I_j-\mu_{k})$ in Eq.(\ref{eq:guidedfilter}) should have a positive sign. Otherwise, it will be negative. Thus the term $1+\frac{(I_i-\mu_{k})(I_j-\mu_{k})}{\sigma_k^2+\epsilon}$ in Eq.(\ref{eq:guidedfilter}), is large for pixel pairs on the same side of the edge and small for pixel pairs on the different side of the edge. Hence, edges are distinguished by different pixel weights.
For an input source image $x$, we use Eq.(\ref{eq:wtsum}) to get a filtered output $x_f$. Afterwards, it is subtracted from the original image to obtain an edge image, $x_e=x-x_f$, which captures the edges well. In the same way, we can get the edge image of the target image, $z_e$.
With the edge images, we can implement the patch matching on them. Mean squared error (MSE) is a widely used distance measure to evaluate similarity of image patches. But the pixel-wise similarity measure is not able to reflect intrinsic image structures, which is a main defect especially when the reference images are just rough edge maps. To solve this problem, we utilize the gradient mean square error, or GMSE for short. Let $p$ be a patch in $x_e$, and $q$ be a patch in $z_e$. The similarity criterion $D(p, q)$ is defined as: \begin{equation} \label{eq:GMSE} D(p, q) = ||p-q||_2^2+\eta||\nabla{p}-\nabla{q}||_2^2. \end{equation} where $\nabla$ is the gradient operator and $\eta$ is a weighting parameter. It emphasizes on both intensity and structure similarity, which is important for our content-oriented matching process. As can be seen from Fig.2, even with single and inconsistent image reference, we are still able to build corresponding image pairs.
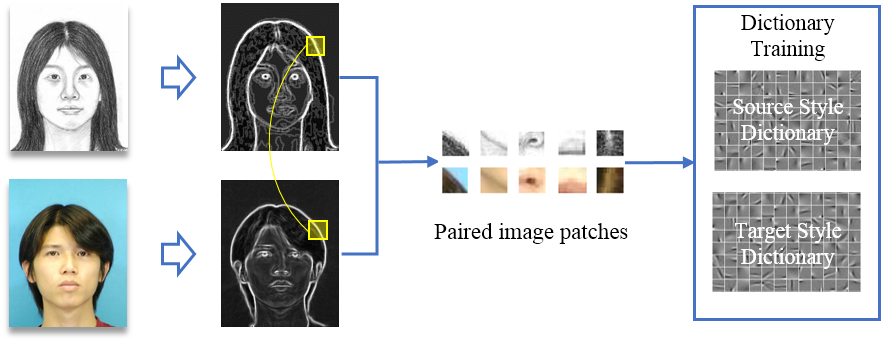
Fig.2 Edge features are used to map patches between different style images for coupled dictionary learning.
Fig.2 depicts the dictionary learning process with the mapped patches. First, the target style image (e.g., a sketch photo) and the source input image are used to generate edge features with guided image filtering. Then, similar patches of two style images are mapped in measure of gradient MSE on edge features. At last, coupled dictionaries are learned on the paired image patches.
Experimental Results
To evaluate the efficiency of the our method, the proposed framework is applied to the typical cross-style transformation application, photo-sketch synthesis. Here we conduct photo-sketch face synthesis on the CUFS Database \footnote{http://mmlab.ie.cuhk.edu.hk/archive/facesketch.html}. Sketches which are often drawn by artists have significantly different appearance from the original photos.

Fig.3 Target image and test input source images from the CUFS database.
We test the proposed method on photo images with a sketch image as target (see Fig.3, the left one serves as target and the right ones are input images). For each input, a coupled edge patch based dictionary is learned separately. The patch size is $7\times7$ and the overlap between patches is [5, 5]. We compare our method with two state-of-the-art methods, Wang et al.'s method [4] and SCDL [5].

Fig.4 Subjective experimental results. (a) Ground truth. (b) Wang et al.'s method [4] without MRF. (c) Wang et al.'s method [4] with MRF. (d) SCDL. (e) The proposed method.
Fig.4 shows subjective results on two test photo images. Note the highlighted part in the comparing images. In contrast with the fully referenced methods, our algorithm achieves similar results with SCDL and outperforms Wang et al.'s method as well. Note that, owing to the texture transfer process, the reconstructed image by the proposed method presents more target-like details.
Reference
[1] K. Jia, X. Wang, and X. Tang, “Image transformation based on learning dictionaries across image spaces,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 35, no. 2, pp. 367–380, Feb. 2013.
[2] H. Bhujle and S. Chaudhuri, “Novel speed-up strategies for non-local means denoising with patch and edge patch based dictionaries,” IEEE Transactions on Image Processing, vol. 23, no. 1, pp. 356–365, Jan. 2014.
[3] K. He, J. Sun, and X. Tang, “Guided image filtering,” in European Conference on Computer Vision. Springer, 2010, pp. 1–14.
[4] X. Wang and X. Tang, “Face photo-sketch synthesis and recognition,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 31, no. 11, pp. 1955–1967, Nov. 2009.
[5] S. Wang, L. Zhang, Y. Liang, and Q. Pan, “Semi-coupled dictionary learning with applications to image super resolution and photo-sketch synthesis,” in IEEE Conference on Computer Vision and Pattern Recognition, Sep. 2012, pp. 2216–2223.